Pythonと機械学習

Pythonも機械学習も初心者ですが、頑張ってこのブログで勉強してこうと思います。

トップ > 機械学習 > 2次計画法

2次計画法

機械学習

ラグランジュ乗数の意味

サポートベクトルのマージンを最大化するために、ラグランジュの未定乗数法を等式制約から不等式制約がある場合に拡張する必要があります。

ラグランジュの未定乗数法を不等式制約がある場合に拡張した最適化アルゴリズムを2次計画法(有効制約法)と言います。

不等式制約を考える上でラグランジュ乗数の意味を理解する必要があります。

等式制約で求まった最適解においては、目的関数の勾配と、制約関数の勾配方向が並行になる性質があります。

f:id:darden:20160830221805p:plain

つまり、適当な定数{\lambda}とおいて以下(1)式が成り立っています。

{\displaystyle
\nabla f(x)= -\lambda\nabla g(x)  \tag{1}
}

(1)式の右辺を左辺に移項してやると、

{\displaystyle
\nabla f(x) + \lambda\nabla g(x)=0  \tag{2}
}

この(2)式はラグランジュ関数を設計変数で微分した値を0とおいた式になります。

ラグランジュの未定乗数法はまさに目的関数と制約関数の勾配が平行になるという性質を利用したアルゴリズムになります。

では、ラグランジュ乗数の意味を考えてみましょう。

ラグランジュ乗数が負の場合は、(1)式より目的関数と制約関数の勾配方向が一致しており、目的関数が減少する方向は、制約関数が減少する方向を意味しています。

反対にラグランジュ乗数が正の場合は、目的関数の勾配は制約関数の勾配と反対方向を向いており、目的関数が減少する方向は、制約関数が増加する方向を意味しています。

ラグランジュ乗数の符号により、目的関数の勾配と制約関数の勾配の向きが一致しているか否かがわかるわけです。

2次計画法のアルゴリズム

不等式制約{\mathbf{g}(\mathbf{x})\leq0}がある場合に、目的関数{f(\mathbf{x})}を最小化することを考えます。

制約関数と目的関数はそれぞれ、設計変数{\mathbf{x}}の1次式、2次式で表されます。

{\displaystyle f(\mathbf{x})=\frac{1}{2}\mathbf{x}^T \mathbf{Q} \mathbf{x} -\mathbf{c}^T \mathbf{x} \tag{3} }

{\displaystyle \mathbf{g}(\mathbf{x}) = \mathbf{A} \mathbf{x} - \mathbf{b} \leq 0 \tag{4} }

目的関数{f(\mathbf{x})}の純粋な最小値(制約条件がない場合の最小値)が、{\mathbf{g}(\mathbf{x})\leq0}内にある場合は、制約条件を考える必要はありません。この場合の制約条件を無効制約と呼びます。

しかし反対に外側にある場合は、少なくとも１つの等式制約式 {\mathbf{g}(\mathbf{x})=0}上に最適解が存在し、更にそのラグランジュ乗数は、目的関数が減少する方向と制約関数が増加する方向が一致する様に定まります。

つまりラグランジュ乗数は正の値になります。この場合の制約条件を有効制約と呼びます。

f:id:darden:20160830221837p:plain

これらの事をまとめると、不等式制約がある場合の目的関数の最小値を与える最適解{\mathbf{x}}とラグランジュ乗数{\mathbf{\lambda}}は以下4つの条件式を満たすことになります。

{\displaystyle \mathbf{Q} \mathbf{x} - \mathbf{c} +\mathbf{A}^T \mathbf{\lambda} =0 \tag{5} }

{\displaystyle \mathbf{a}_i \mathbf{x} - b_i \leq 0 ~~~~(i=1,2,\cdots,m) \tag{6} }

{\displaystyle \lambda_i \geq 0 ~~~~(i=1,2,\cdots,m) \tag{7} }

{\displaystyle \lambda_i(\mathbf{a}_i \mathbf{x} - b_i)=0 ~~~~(i=1,2,\cdots,m) \tag{8} }

添え字の{i}は、制約条件の番号を表しています。制約条件は全部で{m}個あるとします。

(6)、(8)式の{\mathbf{a}_i}は、{\mathbf{A}}マトリックスの{i}番目の行を横ベクトルとして表したもので、

{\displaystyle
\begin{eqnarray}
\mathbf{a}_i=\left[
\begin{array}{cccc}
a_{i1} & a_{i2} & \cdots & a_{in} 
\end{array}
\right]
\end{eqnarray}  \tag{9}
}

{n}は、設計変数の個数です。つまり、

{\displaystyle
\begin{eqnarray}
\mathbf{A}=\left[
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{array}
\right]

=\left[
\begin{array}{c}
\mathbf{a}_1 \\
\vdots \\
\mathbf{a}_i \\
\vdots \\
\mathbf{a}_m
\end{array}
\right]

\end{eqnarray}  \tag{10}
}

(5)、(6)、(7)、(8)の4つの式はKKT条件(Karush-Kuhn-Tucker条件)と呼ばれています。

(5)式は、目的関数と制約関数の勾配が平行であることを表し、(6)式は不等式制約そのままです。

(7)式は、最適解{\mathbf{x}}が無効制約上にある場合は{\lambda_i=0}になり、有効制約上にある場合は{\lambda_i>0}になることを表しています。

(8)式は、最適解{\mathbf{x}}が無効制約上にある場合は{\lambda_i=0}、有効制約上にある場合は{\mathbf{a}_i \mathbf{x} - b_i =0}になるので、{\lambda_i}と{\mathbf{a}_i \mathbf{x} - b_i}をかけてやると、その値は常に0になることを表しています。

2次計画法では、それぞれのKKT条件を満たすように逐次的に{\mathbf{x}}を動かしてやります。

全てのKKT条件が満たされた{\mathbf{x}}を発見できた場合はそれが、最適解になります。

以下最適化ルーチンをステップ別で分けていきます。

Step1

先ずは動かしてやる設計変数の初期値{\mathbf{x}_0}を適当に決めてやります。(取りあえずは0ベクトルでいいです。)

その後、{\mathbf{x}_0}を少しずつ動かして、(6)式で表される全ての不等式制約を満たす{\mathbf{x}}を見つけてやります。

(6)式を全て満たす{\mathbf{x}}を実行可能解といいます。

実行可能解が見つかったら、有効制約となる制約条件{\mathbf{a}_i \mathbf{x} - b_i=0}があるかどうかを調べます。もし有効制約となる制約条件が見つかったらその制約条件の番号をリスト{\mathbf{W}}に保存しておきます。

Step2

有効制約となる制約条件が見つかった場合、{\mathbf{A}}と{\mathbf{b}}から無効制約となる行を取り除き、有効制約のみで作り直して{\mathbf{A}_q}と{\mathbf{b}_q}としてやります。

{\displaystyle
\begin{eqnarray}
\mathbf{A}_q=\left[
\begin{array}{c}
\vdots \\
\mathbf{a}_i \\
\vdots \\
\end{array}
\right]
\end{eqnarray}  
~~~~(i\in \mathbf{W}) \tag{11}
}

{\displaystyle
\begin{eqnarray}
\mathbf{b}_q=\left[
\begin{array}{c}
\vdots \\
b_i \\
\vdots \\
\end{array}
\right]
\end{eqnarray}
~~~~(i\in \mathbf{W}) \tag{12}
}

有効制約で作り直した{\mathbf{A}_q}、{\mathbf{b}_q}及び{\mathbf{Q}}、{\mathbf{c}}より、ラグランジュの未定乗数法を使って一時的な解{\hat{\mathbf{x}}}とラグランジュ乗数{\hat{\mathbf{\lambda}}}を求めてやります。

{
\displaystyle
\begin{eqnarray}
\left[
\begin{array}{c}
\hat{\mathbf{x}}   \\
 \hat{\mathbf{\lambda}} \\
\end{array}
\right]

=\left[
\begin{array}{cc}
\mathbf{A}_q & \mathbf{0}  \\
\mathbf{Q} & \mathbf{A}_q^T \\
\end{array}
\right]^{-1}
\left[
\begin{array}{c}
\mathbf{b}_q   \\
\mathbf{c}  \\
\end{array}
\right]
\end{eqnarray}   \tag{13}
}

有効制約となる制約条件が見つからなかった場合は、{\mathbf{A}_q}と{\mathbf{b}_q}を考慮する必要がなく{\mathbf{Q}}、{\mathbf{c}}のみで制約条件がない場合の純粋な目的関数の最小解を{\hat{\mathbf{x}}}とし、ラグランジュ乗数{\hat{\mathbf{\lambda}}}は0にしておきます。

{
\displaystyle
\begin{eqnarray}
\left[
\begin{array}{c}
\hat{\mathbf{x}}   \\
 \hat{\mathbf{\lambda}} \\
\end{array}
\right]

=\left[
\begin{array}{c}
\mathbf{Q}^{-1}  \\
\mathbf{0}
\end{array}
\right]
\left[
\begin{array}{c}
\mathbf{c}
\end{array}
\right]
\end{eqnarray}   \tag{14}
}

求めた{\hat{\mathbf{x}}}が実行可能解でない場合はStep3へ進み、実行可能解である場合はStep4へ進みます。

Step3

実行可能解の領域外に出てしまった{\hat{\mathbf{x}}}を、有効制約上に乗るように実行可能解に戻してやります。

Step1で求めた{\mathbf{x}}は実行可能解であるため、実行可能解領域外に出てしまった{\hat{\mathbf{x}}}と{\mathbf{x}}を結ぶ直線上に少なくとも一つは、有効制約となる{\hat{\mathbf{x}}'}が存在します。

{\hat{\mathbf{x}}}と{\mathbf{x}}を結ぶ直線上の点{\hat{\mathbf{x}}'}は、{t~(0\leq t \leq1)}を用いて以下の様に表すことができます。

{
\displaystyle
\hat{\mathbf{x}}'= \mathbf{x} +t(\hat{\mathbf{x}} - \mathbf{x})  \tag{15}
}

f:id:darden:20160902223745p:plain

{\hat{\mathbf{x}}'}を少なくとも一つの有効制約上に乗せてやるため、{\mathbf{g}(\hat{\mathbf{x}}')=0}の中で、{0\leq t \leq1}でかつ一番小さな{t}を見つけてやります。

つまり、{m}個ある制約関数すべてに{\hat{\mathbf{x}}'}を入れてやり、その値を0と置いて各式で{t}を求めてやり、0以上でかつ最小になる{t}を一つだけ求めます。

{
\displaystyle
g_i(\hat{\mathbf{x}}')= \mathbf{a}_i \left[ \mathbf{x} +t_i(\hat{\mathbf{x}} - \mathbf{x}) \right] - b_i=0  \tag{16}
}

{
\displaystyle
\begin{align}
\therefore ~~~
t_i &= \frac{-(\mathbf{a}_i \mathbf{x} - b_i)}{\mathbf{a}_i (\hat{\mathbf{x}} - \mathbf{x}) } \\

&= \frac{-g_i(\mathbf{x})}{\mathbf{a}_i (\hat{\mathbf{x}} - \mathbf{x}) }
\tag{17}
\end{align}
}

{
\displaystyle
\Rightarrow ~~~
t = \min_{0\leq t_i \leq 1} t_i~~~~~(~i=1,2,\cdots,m ~)
\tag{18}

}

(18)式で求まった{t}を使って、(15)式より{\hat{\mathbf{x}}'}を求めた後、{\hat{\mathbf{x}}'}を新しい{\mathbf{x}}として更新します。

この時有効制約が一つ増えているので、その有効制約条件番号をリスト{\mathbf{W}}に追加してStep2に戻ります。

Step4

Step2で求めた{\hat{\mathbf{x}}}が実行可能解であり、更に同時に求めた{\hat{\mathbf{\lambda}}}の全ての値が(7)式{\lambda_i \geq 0 ~~~~(i=1,2,\cdots,m)}を満たすとき、全てのKKT条件が満たされたことになり、{\hat{\mathbf{x}}}は最適解となっています。

{\hat{\mathbf{x}}}を最適解として出力し、ループを終了します。

{\lambda_i}＜{~0~}がある場合は、その中で一番小さな{\lambda_i}の制約条件番号{i}をリスト{\mathbf{W}}から取り除いてStep2に戻りループを繰り返します。

初期実行可能解の求め方

Step1で適当に決めてやった設計変数の初期値{\mathbf{x}_0}を実行可能解に移動させる方法を考えてみました。

先ず、{\mathbf{x}_0}を制約関数{\mathbf{g}(\mathbf{x})}に代入し、{\mathbf{g}(\mathbf{x}_0)}＞{~0~}の中で一番大きな値を持つ、{g_i(\mathbf{x}_0)}を見つけてやります。

今、{i}番目の制約関数値{g_i(\mathbf{x}_0)}が一番大きかったとして、{\mathbf{x}_0}を{g_i(\mathbf{x}) \leq 0}の内側に持ってくることを考えます。

点{\mathbf{x}_0}と直線{g_i(\mathbf{x})＝\mathbf{a}_i \mathbf{x} -b_i = 0}の距離{\mathbf{d}_i}は、

{
\displaystyle
\mathbf{d}_i = \frac{|\mathbf{a}_i \mathbf{x}_0 -b_i|}{||\mathbf{a}_i||}
\tag{19}
}

また、{g_i(\mathbf{x})＝\mathbf{a}_i \mathbf{x} -b_i}が減少する方向は、

{
\displaystyle
-\nabla g_i(\mathbf{x}) = -\frac{\partial (\mathbf{a}_i \mathbf{x} -b_i)}{\partial \mathbf{x}}= -\mathbf{a}_i^{T}
\tag{20}
}

(20)式で表される方向に対して、(19)式で表される距離よりも少し長く動かしてやれば、{\mathbf{x}_0}を{g_i(\mathbf{x}) \leq 0}の内側に持ってくることができます。

1より少し大きい適当な定数を{\alpha}とすると、{\mathbf{x}_0}をアップデートする点{\mathbf{x}_0'}は、

{
\displaystyle
\mathbf{x}_0' = -\alpha \frac{|\mathbf{a}_i \mathbf{x}_0 -b_i|}{||\mathbf{a}_i||^2} \mathbf{a}_i^{T}
\tag{21}
}

になります。

この操作を繰り返していくと、そのうち全ての制約条件を満たす実行可能解を見つけることができます。

ただし、{i}番目の制約関数値{g_i(\mathbf{x})}が減少する方向{-\mathbf{a}_i^{T}}は、他の制約関数が減少する方向というわけではないので、この操作をずっと繰り返しても、必ずしも実行可能解が見つかるわけではないです。本来はもっとうまい方法があると思いますが、取りあえずはこの方法を採用しました。

Pythonでコーディング

2次計画法で不等式制約がある場合の目的関数を最小化するコードを書いてみました。

設計変数の個数と制約条件の個数はどちらも2個として、main関数の中で以下4つの簡単なケースにおける最適化結果を出力します。

  • 2つある制約条件のうちどちらも無効制約条件の場合
  • 2つある制約条件のうち1つが有効制約条件の場合(2番目の制約条件が有効制約)
  • 2つある制約条件のうちどちらも有効制約条件の場合
  • 目的関数と制約関数を乱数で作成した場合
2つある制約条件のうちどちらも無効制約条件の場合

目的関数と制約条件が以下の場合を考えます。

{\displaystyle f(\mathbf{x})=x_1^2+x_2^2 }

{\displaystyle g_1(\mathbf{x}) = x_1+x_2 -1 \leq 0 }　

{\displaystyle g_2(\mathbf{x}) = -x_1+x_2 -1 \leq 0 }　

{\mathbf{x},\mathbf{c},\mathbf{Q},\mathbf{b},\mathbf{A}}は以下のようになります。

{
\displaystyle
\begin{eqnarray}
\mathbf{x}=\left[
\begin{array}{c}
x_{1} \\
x_{2} 
\end{array}
\right]
,~~
\mathbf{c}=\left[
\begin{array}{c}
0 \\
0 
\end{array}
\right]
,~~
\mathbf{Q}=\left[
\begin{array}{cc}
2 & 0 \\
0 & 2
\end{array}
\right]
,~~
\mathbf{b}=\left[
\begin{array}{c}
1 \\
1
\end{array}
\right]
,~~
\mathbf{A}=\left[
\begin{array}{cc}
1 & 1 \\
-1 & 1
\end{array}
\right]
\end{eqnarray}
}

制約条件{g_1(\mathbf{x})\leq 0}、{g_2(\mathbf{x})\leq 0}はどちらも無効制約になるので、目的関数{f(\mathbf{x})}の最小値は、制約がない場合の最小値になります。最適解は{(x_1,x_2) = ( 0.0,0.0)}です。

f:id:darden:20160905211442p:plain

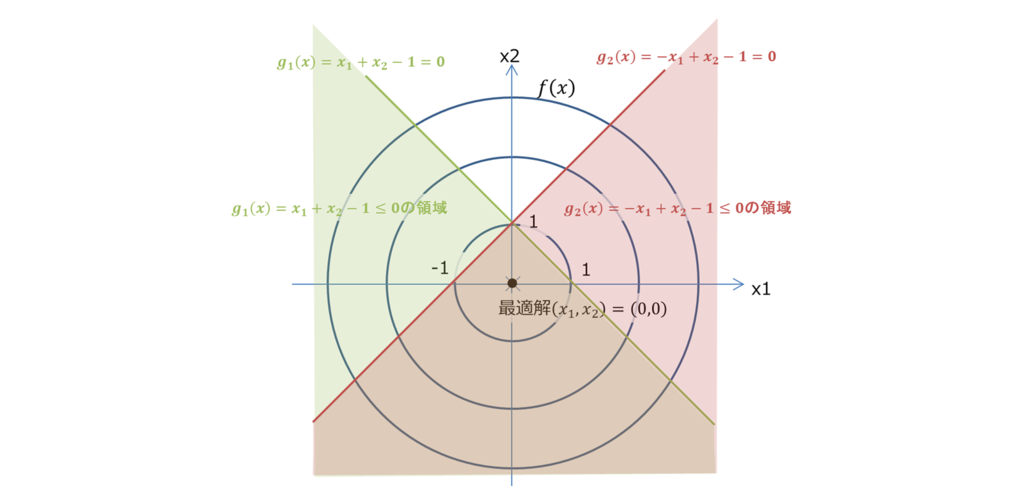
以下スクリプトの実行結果です。あってますね。

■2つある制約条件のうちどちらも無効制約条件の場合
1回目のイタレーションで最適解が見つかりました。
・最適解x: [0.0, 0.0]
・目的関数f(x)の最小値: 0.0
・KKT条件1(∇f+λ∇g=0): True [0.0, 0.0]
・KKT条件2(g<=0): True [-1.0, -1.0]
・KKT条件3(λ>=0): True [0.0, 0.0]
・KKT条件4(λg=0): True [0.0, 0.0]
2つある制約条件のうち1つが有効制約条件の場合(2番目の制約条件が有効制約)

以下、目的関数と制約条件です。

{\displaystyle f(\mathbf{x})=x_1^2+x_2^2 }

{\displaystyle g_1(\mathbf{x}) = x_1+x_2 -1 \leq 0 }　

{\displaystyle g_2(\mathbf{x}) = -x_1+x_2 +1 \leq 0 }　

{\mathbf{x},\mathbf{c},\mathbf{Q},\mathbf{b},\mathbf{A}}は以下のようになります。

{
\displaystyle
\begin{eqnarray}
\mathbf{x}=\left[
\begin{array}{c}
x_{1} \\
x_{2} 
\end{array}
\right]
,~~
\mathbf{c}=\left[
\begin{array}{c}
0 \\
0 
\end{array}
\right]
,~~
\mathbf{Q}=\left[
\begin{array}{cc}
2 & 0 \\
0 & 2
\end{array}
\right]
,~~
\mathbf{b}=\left[
\begin{array}{c}
1 \\
-1
\end{array}
\right]
,~~
\mathbf{A}=\left[
\begin{array}{cc}
1 & 1 \\
-1 & 1
\end{array}
\right]
\end{eqnarray}
}

{g_1(\mathbf{x})\leq 0}が無効制約、{g_2(\mathbf{x})\leq 0}が有効制約になります。グラフから最適解が{(x_1,x_2) = ( 0.5,-0.5)}になるのが直感でわかると思います。

f:id:darden:20160905211501p:plain

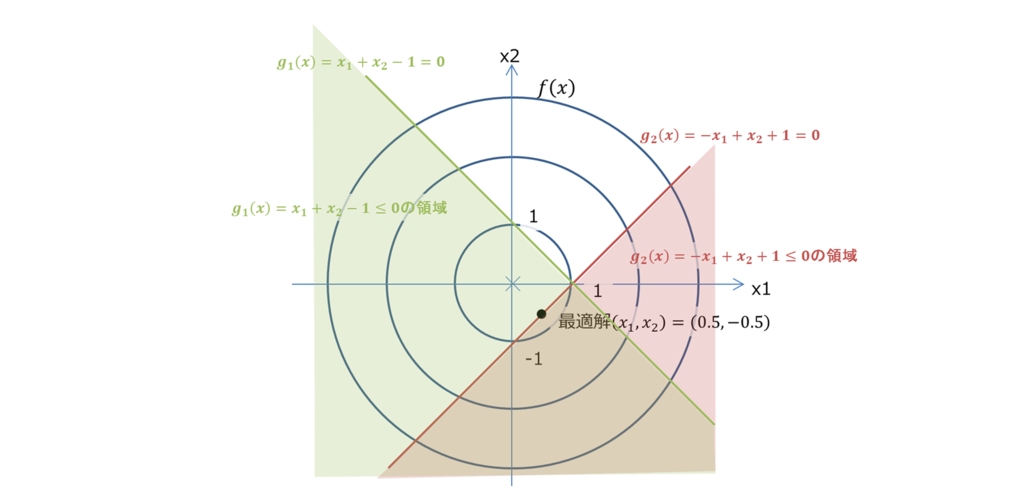
以下スクリプトの実行結果です。まあ、あってます。

■2つある制約条件のうち1つが有効制約条件の場合(2番目の制約条件が有効制約)
2回目のイタレーションで最適解が見つかりました。
・最適解x: [0.5, -0.5]
・目的関数f(x)の最小値: 0.5
・KKT条件1(∇f+λ∇g=0): True [0.0, 0.0]
・KKT条件2(g<=0): True [-1.0, 0.0]
・KKT条件3(λ>=0): True [0.0, 1.0]
・KKT条件4(λg=0): True [0.0, 0.0]

　

2つある制約条件のうちどちらも有効制約条件の場合

以下、目的関数と制約条件です。

{\displaystyle f(\mathbf{x})=x_1^2+x_2^2 }

{\displaystyle g_1(\mathbf{x}) = x_1+x_2 +1 \leq 0 }　

{\displaystyle g_2(\mathbf{x}) = -x_1+x_2 +1 \leq 0 }　

{\mathbf{x},\mathbf{c},\mathbf{Q},\mathbf{b},\mathbf{A}}は以下のようになります。

{
\displaystyle
\begin{eqnarray}
\mathbf{x}=\left[
\begin{array}{c}
x_{1} \\
x_{2} 
\end{array}
\right]
,~~
\mathbf{c}=\left[
\begin{array}{c}
0 \\
0 
\end{array}
\right]
,~~
\mathbf{Q}=\left[
\begin{array}{cc}
2 & 0 \\
0 & 2
\end{array}
\right]
,~~
\mathbf{b}=\left[
\begin{array}{c}
-1 \\
-1
\end{array}
\right]
,~~
\mathbf{A}=\left[
\begin{array}{cc}
1 & 1 \\
-1 & 1
\end{array}
\right]
\end{eqnarray}
}

{g_1(\mathbf{x})\leq 0}、{g_2(\mathbf{x})\leq 0}どちらも有効制約になります。こちらもグラフから最適解が{(x_1,x_2) = ( 0,-1)}になるのが直感でわかると思います。

f:id:darden:20160905211514p:plain

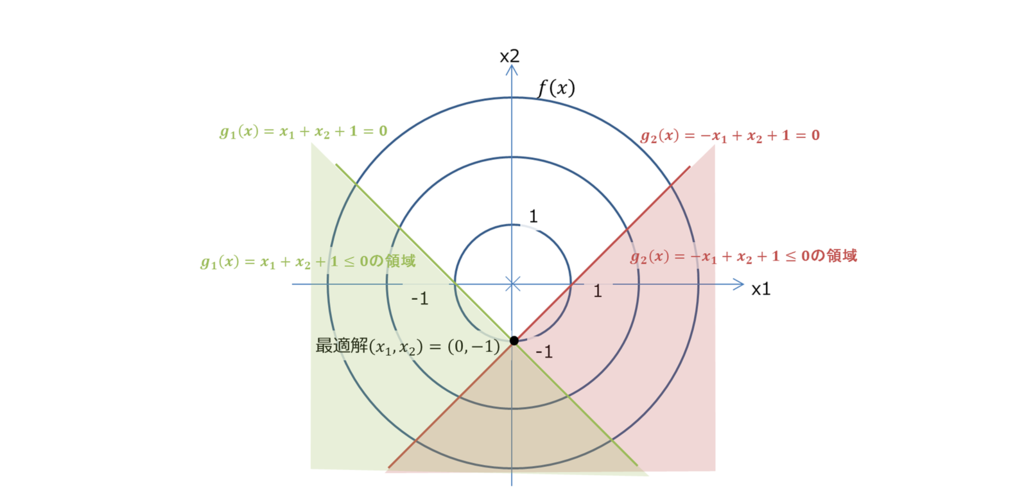
以下スクリプトの実行結果です。あってますね。

■2つある制約条件のうちどちらも有効制約条件の場合
2回目のイタレーションで最適解が見つかりました。
・最適解x: [0.0, -1.0]
・目的関数f(x)の最小値: 1.0
・KKT条件1(∇f+λ∇g=0): True [0.0, 0.0]
・KKT条件2(g<=0): True [0.0, 0.0]
・KKT条件3(λ>=0): True [1.0, 1.0]
・KKT条件4(λg=0): True [0.0, 0.0]
目的関数と制約関数を乱数で作成した場合

最後に、目的関数と制約関数を乱数で作成した場合を試してみました。

{\mathbf{c},\mathbf{Q},\mathbf{b},\mathbf{A}}を乱数で作成しています。

以下スクリプトの実行結果です。一応KKT条件をすべて満たしているので、最適解は求まっているみたいです。

■目的関数と制約関数を乱数で作成した場合
1回目のイタレーションで最適解が見つかりました。
・最適解x: [-44.55150263525623, -20.471794551317355]
・目的関数f(x)の最小値: 18.1186729545
・KKT条件1(∇f+λ∇g=0): True [-3.885780586188048e-16, 2.220446049250313e-16]
・KKT条件2(g<=0): True [-44.92869339177389, -14.731499126102424]
・KKT条件3(λ>=0): True [0.0, 0.0]
・KKT条件4(λg=0): True [0.0, 0.0]

たまに1000回イタレーションループを回しても計算が収束しないときがあります。また、制約条件の数を増やしすぎると初期実行解が見つけられなくなるので、まだ工夫の余地はあるでしょうね。

参考にさせていただいたサイト