再帰型強化学習
目次
はじめに
こちらのブログで紹介されている、再帰型強化学習を使ってFXトレードをしてみるという記事が面白そうだったので試してみることにしました。
再帰型強化学習について知識はゼロですが、取り敢えずやってみるというのが大事じゃないかと思います。
強化学習とは機械学習の一種で、エージェントがアクションを起こして、そのアクションによって報酬をもらえるというような仕組みみたいで、各アクションでもらえる報酬を最大化するように学習を実施するという物らしいです。
更に再帰型なので、なんかよくわからなくてすごそうです。英語(Recurrent Reinforcement Learning)の頭文字をとってRRLと呼ばれてるみたいです。
上記のブログで参考にしてた論文がリンクされていたので、取り敢えずそちらを見ながら数式を追ってみることにしました。
再帰型強化学習のアルゴリズム
先ず、エージェント(ボットに相当します)のアクションですが、時刻におけるアクションを
で表しlongかshortかneutral(それ以外)の3通りで、それぞれ数字の1、-1、0を割り当てます。要するに買うか、売るか、何もしない(ポジションを持たない)かの3通りです。
時刻におけるアクション
は、
より前の
個の各時刻の価格変動
と、一つ前の時刻のアクション
に適当な重み
をかけて足し合わせた後、ハイパブリックタンジェントの出力として表します。
は時刻
の価格です。ちょっとパーセプトロンっぽいです。
(3)式の一番左の1はしきい値を考慮したものです。M個の価格変動値とひとつ前のアクション
と合わせて、
は、全部でM+2個の成分からなるベクトルになります。
必然的に重みもM+2個の成分を持つベクトルになります。
現在のアクションを決定するために、一つ前の時間のアクション
が必要なところが再帰型というわけですね。
時刻においてもらえる報酬
は、取引量
とスプレッド
を使って以下のようにかけます。
基本的には、エージェントは各時刻で報酬が大きくなるようなアクション
をとるように学習すればいいと思いますが、上記の論文では、ある学習期間
内で定義されるシャープレシオ
というものを考え、それを最大化するように学習するみたいです。
シャープレシオは、期間
内での
の平均と標準偏差の比で表されます。
標準偏差は、2乗平均と平均
の2乗の差で表すことができるので以下の様に書くことができます。
確かに一回あたりの取引でもらえる報酬の平均が大きいほど、更にそのバラツキである標準偏差が小さいほど確実な利益を確保できるので、このシャープレシオという指標を最大化することは理にかなっています。
重みを変化させることで各時刻のアクションが変化し、その結果シャープレシオが変化するので、シャープレシオの重みに対する勾配
を算出し、その勾配方向に向かって重みを少しずつ変化させてやることでシャープレシオを最大化させる事ができます。
コスト関数がシャープレシオになり、勾配降下法が勾配上昇法になってますが、学習方法はADALINEなんかとにてますね。
シャープレシオの重みに対する勾配を求める為に、シャープレシオを重みで微分しなければいけません。これがまた大変ですね。。
シャープレシオは、平均
と2乗平均
の関数で、更に
と
は
の関数で、更に
は
の関数で、
がようやく重み
の関数なので、シャープレシオに対し随分深いところに重み
がいます。
こういった関数の中に関数があって更にその中に関数があって、、という場合の微分はチェーンルールという方法を使うと簡単(でもないですが。。)に展開する事ができます。
各成分について具体的に求めていきます。
と
は、符号関数
を使って以下の様に書けます。
続いてと
を求めてみましょう。
(16)式より、は、
(10)式から(17)式を全部計算し(9)式に代入することで、の値を計算し、学習率
をかけて、足しこむことで重みをアップデートしていきます。
の算出式(5)では、
が1と-1と0に量子化された値として見てますが、論文中の実際の計算では
は実数として扱っているようです。
を量子化された値として考えると、量子化関数のクォンタライザーも
で微分しなけらばならず、よく分からないことになるからだと思います。
またの算出式(4)や、
と
の算出式(16)、(17)では再帰的に前の値に依存しているので、実際の計算では初期値が必要になってきます。
の初期値を
を0と置き、
の初期値
を0ベクトルと置いてやればいいです。
と
は、重み
と同じ個数(M+2個)の成分を持つベクトルになります。
必然的にもM+2個の成分を持つベクトルです。
Pythonで実装してみる
論文中では、IBMの日足データを使って、過去のある期間でシャープレシオを最大化するよう重み
を学習させ、そこから未来の期間
で最適化した重み
を使って取引したらどうなるか?という検証をしています。
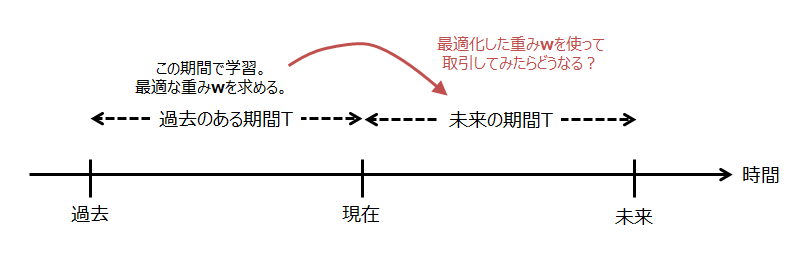
IBMの日足データでは、どうやら効果があるみたいです。
私は出来ればFXで実装したかったので、ブログに合わせてUSDJPYの30分足で検証してみることにしました。
MT4で出力したデータをGistにアップ(USDJPY30.csv)しています。
USDJPY30.csvは、日付、時間、始値、高値、安値、終値、出来高の順でデータが並んでいます。
スクリプト中では、まずUSDJPY30.csvのデータを全部読み込んで、日付と終値をall_t、all_pという変数に保存します。
過去になる程インデックスが大きくなるように設定しています。(単にそうした方が私にとって扱い安いので。) スクリプト中では、tより過去はt+1で表現しているので注意してください。
13行目のinit_tで現在の時間インデックスを指定し、そこから過去の期間T(15行目のT=1000)の価格データをall_t、all_pから切り出して学習を実施します。
学習後は、最適化された重みを使って未来の期間Tの価格データを再びall_t、all_pから切り出し、取引シミュレーションするという流れです。
学習前の重みの初期値は、取り敢えず全部1にしておきました。
検証結果
学習では全部で10000回のエポックを回しており、100エポック毎にシャープレシオと経過時間を出力する様にしています。
Epoch loop start. Initial sharp's ratio is -0.0135567256889. Epoch: 100/10000. Shape's ratio: 0.0343913902529. Elapsed time: 13.3904920599 sec. Epoch: 200/10000. Shape's ratio: 0.0554093411079. Elapsed time: 26.6309506066 sec. ... ... ... Epoch: 9900/10000. Shape's ratio: 0.166130877648. Elapsed time: 1308.91061026 sec. Epoch: 10000/10000. Shape's ratio: 0.166027379068. Elapsed time: 1321.8811445 sec. Epoch loop end. Optimized sharp's ratio is 0.166027379068. Epoch: 10000/10000. Shape's ratio: 0.166027379068. Elapsed time: 1321.88194105 sec.
結構時間かかりますね。。
シャープレシオの推移
以下シャープレシオの推移です。学習率は1で実施しました。
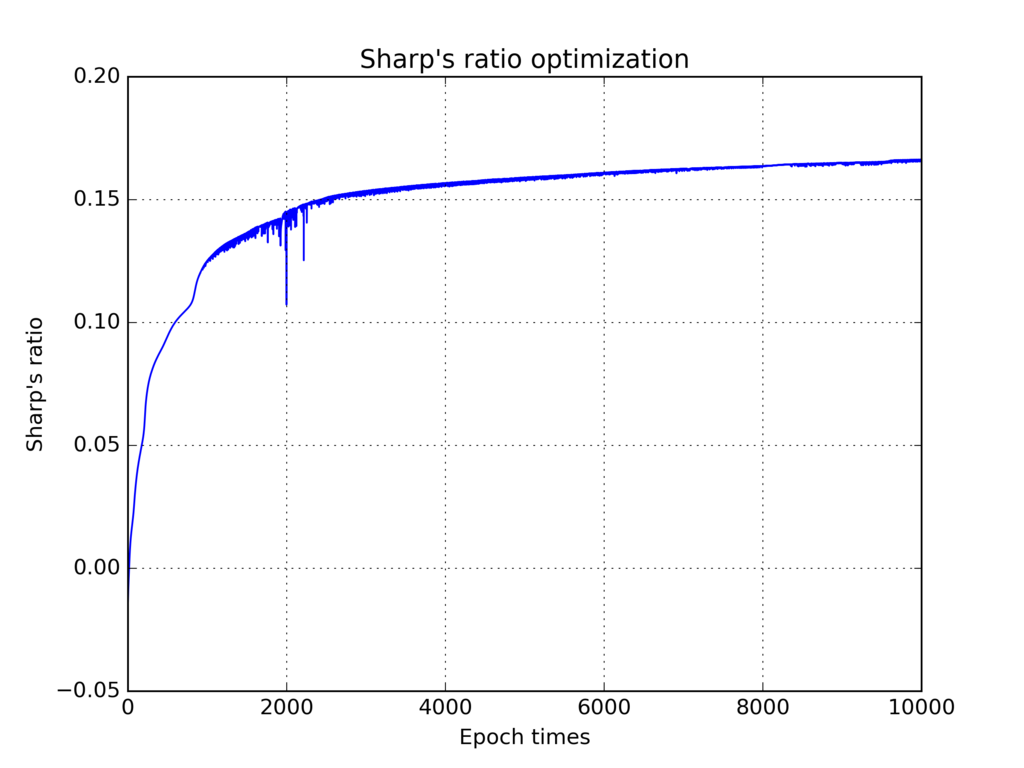
途中で少し値が飛んでますが、エポック数が増えるに従いちゃんとシャープレシオが増えてますね。取りあえずは問題ないようです。
過去の期間Tでの学習結果
以下が過去の期間Tでの学習結果です。上から順にUSDJPYの価格、アクション、報酬
の累積和です。
青い線が学習前の重み(全部1)でトレードを実施した結果で、赤い線が学習後の最適化された重みでトレードを実施した結果です。
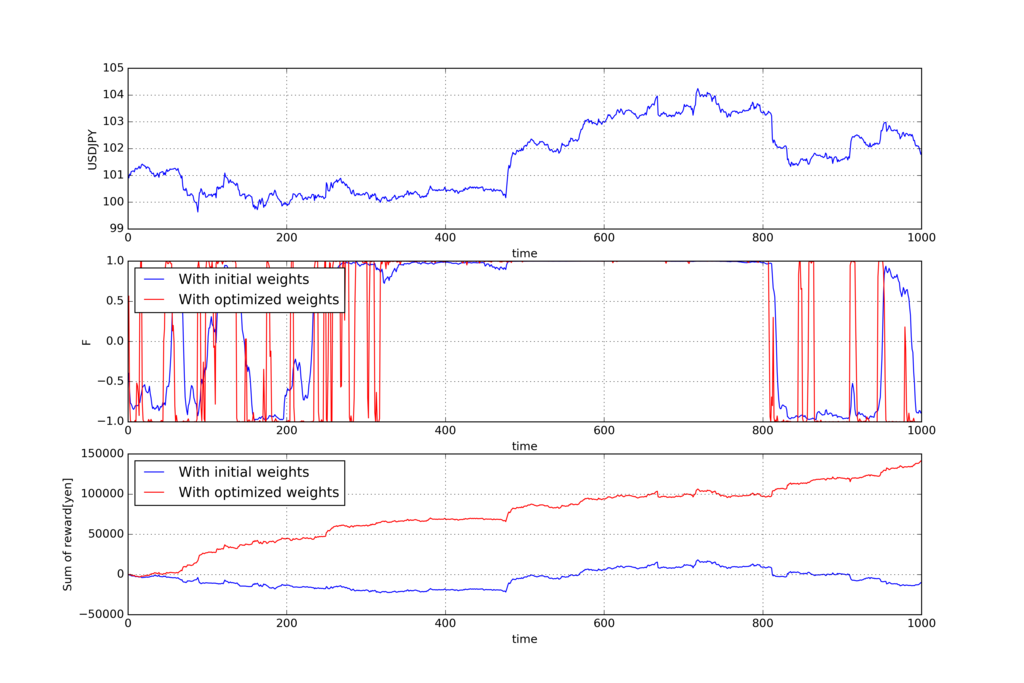
学習後は、報酬の累積和が右肩上がりで増えてますね。
うまく学習できているみたいです。
未来の期間Tでの取引シミュレーション結果
ではこの学習した重みを使って、未来の期間Tでトレードしてみたらどうなるか検証してみましょう。
こちらも上から順にUSDJPYの価格、アクション、報酬
の累積和です。
青い線が全部1の重みでトレードを実施した結果で、赤い線が先ほどの過去の期間Tで学習した重みを使ってトレードを実施した結果です。
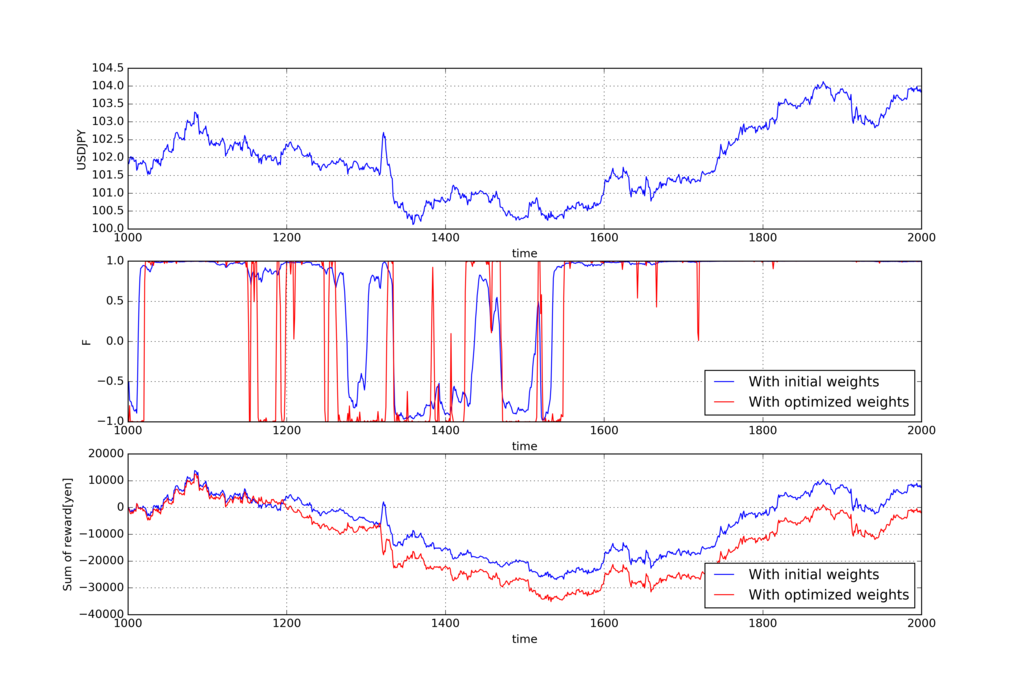
?。報酬の累積和をみると、学習した重みで実施したトレードの方が悪い結果になってますね。。ロバスト性はあまりないようです。
取り敢えずパラメータである期間と重みにかける過去データの個数
の値を最適化してみたい所ですが、私の環境では10000回のエポックループを回すのに1300秒もかかってしまいます。
先ずは学習スピードを何とかして速くするのが先決ですね。愈々Cythonを使ってみようかな。