RRLの学習にGAを使ってみる
目次
はじめに
前回、前々回で遺伝的アルゴリズム(Genertic Algorithm: GA)について書きましたが、そもそもの動機はこのGAを機械学習の重み最適化に使えないだろうか?というものでした。
例えばですが、RRLの再帰部分は通常1回分の過去のアクションを入れてやりますが、過去10回分のアクションを入力するモデルにしたらもっと賢いエージェントになるんじゃないかな?と思ってしまいます。(あまり根拠はないですが直感的に。。)
RRLの詳細についてはこちらの過去記事を参照して下さい。
通常RRLではエージェントの学習に勾配上昇方を使う為、シャープレシオの重み勾配を前もって求める必要がありますが、過去10回分のアクションを入力した場合、このシャープレシオの勾配って求める事ができるのでしょうか?
頑張れば行けるかもしれませんが。。エージェントが更に賢くなる保証もないですし、あんまり頑張りたくないのが本音です。
そう言う場合にGAの登場というわけです。
ということで今回は、RRLの学習における重み最適化にGAを使ったらどうなるか試してみたいと思います。
RRLスクリプト
GA学習版のRRLスクリプトは、以前書いた中でも最高パフォーマンスのCythonラッピングしたC++コードを元にしようと思います。
C++コードのCythonラッピングに関しては以下を参照。
スクリプトはGitHubにあげています。こちらのスクリプトに変更を加えていきます。
重要なファイルは、以下の5つでそれ以外は2次的に生成されるの物なので全部消してOKです。
- tradingrrl_.h:RRLエージェントクラス宣言
- tradingrrl_.cpp:RRLエージェントクラス定義
- tradingrrl.pyx:上記C++コードのCythonラッピングコード
- setup.py:上記Cythonコードのコンパイル用設定
- main.py:RRL学習実施と結果表示
スクリプトの変更点
上記のコードのRRLエージェントクラスのではシャープレシオの重み勾配をメンバ関数calc_dSdw()で求めていて、関数内の途中でシャープレシオSを求めています。
以下calc_dSdw()の定義部です。tradingrrl_.cppの152~181行目です。
void cppTradingRRL::calc_dSdw(){
set_x_F();
calc_R();
calc_sumR();
A = sumR[0]/T;
B = sumR2[0]/T;
S = A/sqrt(B-A*A);
dSdA = S*(1+S*S)/A;
dSdB = -S*S*S/2/A/A;
dAdR = 1.0/T;
for(int j=0 ; j<M+2; ++j ){
dFpdw[j] = 0.0;
dFdw[j] = 0.0;
dSdw[j] = 0.0;
}
for(int i=T-1 ; i>=0 ; --i ){
dBdR[i] = 2.0/T*R[i];
dRdF[i] = - mu*sigma*sign(F[i] - F[i+1]);
dRdFp[i] = mu*r[i] + mu*sigma*sign(F[i] - F[i+1]);
for(int j=0 ; j<M+2; ++j ){
if(i!=T-1){
dFpdw[j] = dFdw[j];
}
dFdw[j]=(1.0 - F[i]*F[i])*(x[i][j] + w[M+2-1]*dFpdw[j]);
dSdw[j]+=(dSdA*dAdR + dSdB*dBdR[i])*(dRdF[i]*dFdw[j] + dRdFp[i]*dFpdw[j]);
}
}
}
GAを使う場合は、シャープレシオの重み勾配まで求める必要がないので、この関数を最後まで実施するのは効率が悪いです。
そこで、重みを引数にしてシャープレシオを返す関数calc_Sを新たに作成してRRLエージェントクラスに追加します。
tradingrrl_.hにメンバ関数の宣言を追加します。
double calc_S(vector<double> _w);
tradingrrl_.cppのメンバ関数の定義はこんな感じです。
double cppTradingRRL::calc_S(vector<double> _w){
w = _w;
set_x_F();
calc_R();
calc_sumR();
A = sumR[0]/T;
B = sumR2[0]/T;
S = A/sqrt(B-A*A);
return S;
}
ラッパーコードtradingrrl.pyxにもメンバ関数の追加を反映させます。
c++クラスの宣言部cdef cppclass cppTradingRRL:に以下の関数宣言を追加し、
double calc_S(vector[double] _w);
c++クラスラッパー部cdef class TradingRRL(object):に以下の関数定義を追加します。
def calc_S(self, vector[double] _w): return self.crrl.calc_S(_w)
続いてmain.pyを変更していきます。(setup.pyは変更点はありません)
RRLの学習をGAで行うga_fitという関数を作成します。以下変更したmain.pyになります。
122~199行目にga_fitの定義を書いています。基本的には前回記事で書いた、遺伝子が連続値の場合のDEAPのチュートリアルスクリプトそのままです。
def ga_fit(_rrl, min_ind, max_ind, random_state, nind, ngen): ... ... return best_ind, logbook
引き数は以下6個です。
- _rrl:RRLエージェントインスタンス
- min_ind:各重みを変更する範囲のmin値
- max_ind:各重みを返送する範囲のmax値
- random_state:乱数のシード
- nind:世代の中の個体数
- ngen:世代ループ数
ベスト解best_indと最適化ログlogbookを戻り値として返すようにしています。
152~153行目の記述で目的関数を定義しています。
def evalOneMax(individual): return _rrl.calc_S(individual),
最適化したいものはシャープレシオになるので、設計変数(個体)に相当する重みindividualを入力して、_rrlインスタンスのシャープレシオを返す関数_rrl.calc_S(individual)をそのまま返すようにしています。
また、各世代ループで実行時間を出力させたかったので、get_elapsedtimeという関数作りました。(189~194行目です)
# Get elapsed time import time tic = time.clock() def get_elapsedtime(data): return time.clock() - tic stats.register("elapsed time",get_elapsedtime)
stats.registerは、世代ループを回すDEAPの関数algorithms.eaSimpleに渡すstats引数を設定する関数で、世代ループ中のログに何を出力するかを登録します。
通常は世代変数populationを引数にとり、世代中の適応度fitnessの状態(平均値、標準偏差、Min値、Max値等)を返すような関数を指定しますが、実行時間は世代変数populationと関係がないので、取りあえず引数で受け取りはしますが実行時間time.clock() - ticだけ返すようにしています。
stats.register("elapsed time",get_elapsedtime)で、"elapsed time"という名前で、get_elapsedtimeの実行結果を出力するようにしています。
重みの変更範囲の設定と学習の実施
31~45行目が、重みの変更範囲の設定と学習の実施部分です。
#--- GA fit #--- Set w ranges. min_w = np.ones(M+2) * -3.0 max_w = np.ones(M+2) * 3.0 #min_w[0] = -5.0 #max_w[0] = 5.0 min_w[M+2-1] = -5.0 max_w[M+2-1] = 5.0 nind = 200 ngen = 170 random_state = 64 best_ind, logbook = ga_fit(rrl, min_w, max_w, random_state, nind, ngen) rrl.w = best_ind rrl.calc_dSdw()
min_w,max_wが、重みの変更範囲のMin値、Max値です。通常の重みは-3.0~3.0、再帰部の1つ前のアクションにかける重みは-5.0~5.0の間で変更するようにしています。
この重みの変更範囲ですが、あまり狭すぎても広すぎても最適化効率が落ちるので絶妙な値を指定する必要があります。
GAによる最適化は、個体中の遺伝子の数nind = 200で、世代ループngen = 170回すようにしています。勾配上昇法で10000回のエポックループを回した時と学習時間が大体同じになるように設定しています。
GAによる学習結果
Cythonスクリプトtradingrrl.pyxを以下のコマンドでコンパイル後、
python setup.py build_ext -i
main.pyを実施すると学習が開始されます。
python main.py
以下学習のログです。
gen nevals avg std min max elapsed time 0 200 -0.365535 0.286895 -0.915838 0.0308361 0.122196 1 112 -0.146748 0.154071 -0.654072 0.0308361 0.201688 2 102 -0.0357136 0.0696521 -0.727766 0.0308361 0.275914 3 133 -0.00843231 0.0343073 -0.392561 0.0416028 0.361662 ... ... ... 167 120 0.135316 0.0449611 -0.28875 0.153046 15.4159 168 111 0.128569 0.0823112 -0.643101 0.153046 15.4848 169 116 0.134146 0.0540075 -0.259718 0.153046 15.5561 170 139 0.133888 0.0570788 -0.514655 0.153046 15.6385
maxが各世代のシャープレシオの最大値、elapsed timeが実行時間です。大体15秒で、シャープレシオが0.153046まで学習できました。
勾配上昇法で学習したとき(過去記事を参照)は、15秒でシャープレシオが0.169771まで学習できているので、勾配上昇法の方が最適化効率は高いんですね。
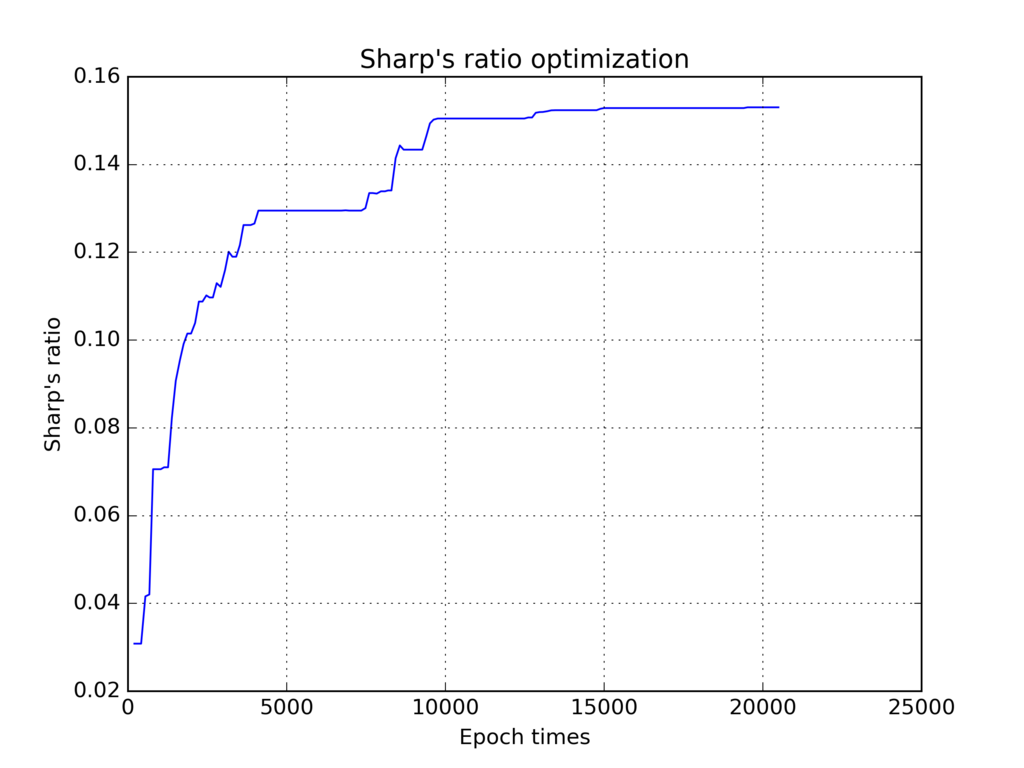
シャープレシオの推移
以下シャープレシオの推移グラフです。学習ログのnevalsに1世代につきアップデートされた個体数が書かれてあるので、これの総和をエポック数としています。まあそれなりに学習できてます。
過去の期間Tでの学習結果
では、肝心の過去の区間での学習状況と、学習した重みを使って未来の区間で取引シミュレーションした結果を見ていきましょう。
以下が過去の期間Tでの学習結果です。上から順にUSDJPYの価格、アクション、報酬
の累積和です。
青い線が学習前の重み(全部1)でトレードを実施した結果で、赤い線が学習後の最適化された重みでトレードを実施した結果です。
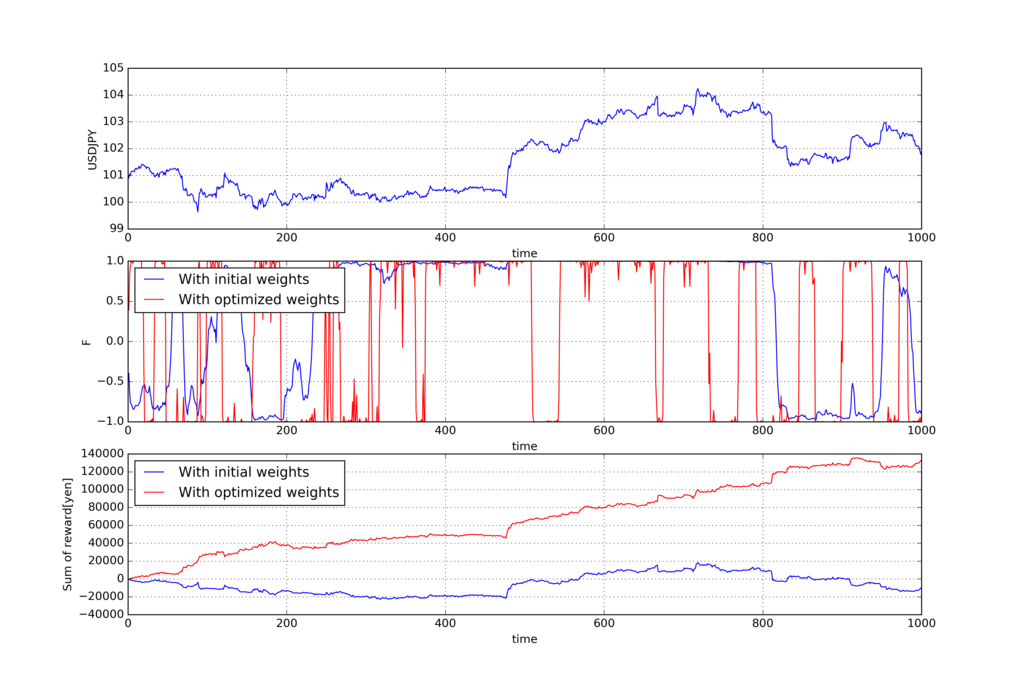
勾配上昇法の時と一緒で、学習後は報酬の累積和が右肩上がりで増えておりうまく学習できています。
未来の期間Tでの取引シミュレーション結果
以下、学習した重みを使って、未来の期間Tでトレードした結果です。
こちらも上から順にUSDJPYの価格、アクション、報酬
の累積和で、青い線が全部1の重みでトレードを実施した結果で、赤い線が先ほどの過去の期間Tで学習した重みを使ってトレードを実施した結果です。
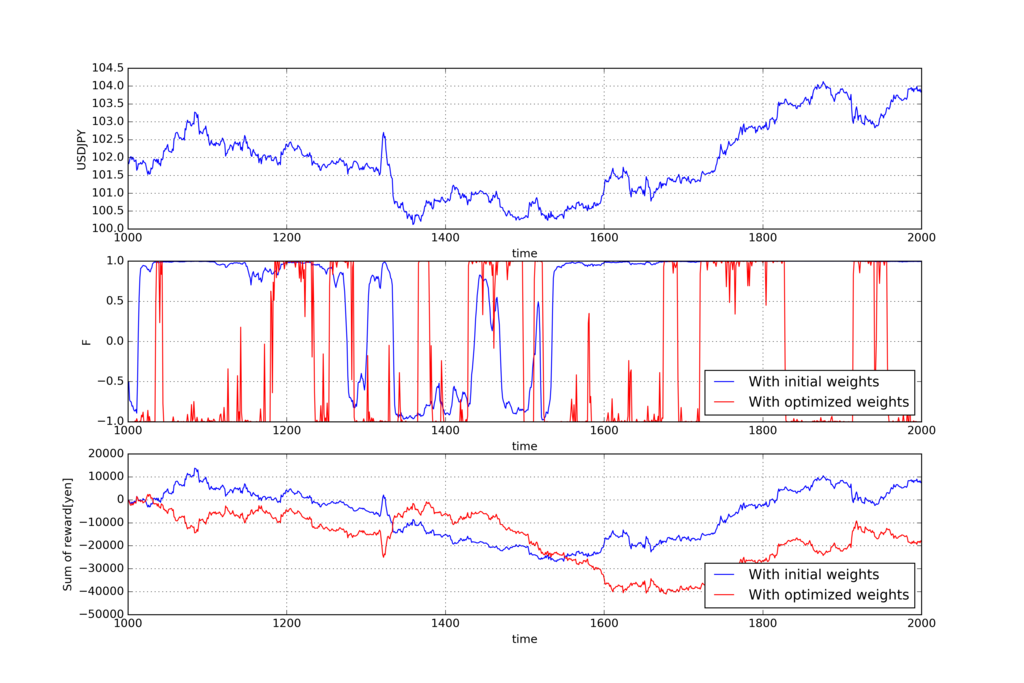
報酬の累積和をみると、学習した重みで実施したトレードの方が悪い結果になっており、こちらも勾配上昇法の時と一緒です。
勾配上昇法の最適解は大抵、極値解に陥っており、一般的にはもっといい解が存在します。一方でGAは大域的な最適解を見つるのが得意なのですが、GAを使ったからと言って、いきなりエージェントが賢くなるわけではないですね。
GAでのネックは、重みの変更範囲をうまく指定しないと最適化がなかなか進まないということですが、勾配上昇法で学習率をうまく設定しないといけないのと一緒なので、そういう意味でいうと勾配上昇法は、手軽さや、最適化効率の面で一番いいのかもしれませんね。
過去10回分のアクションを入力してみる
通常のRRLは過去1回分のアクションを入力して現在のアクションを決定しますが、過去10回分のアクションをRRLに入力したらどうなるか試してみました。
変更部分は、重みwと入力ベクトルx、アクションFの配列の個数を9個増やしてやるだけなので、そんなに難しくはありません。
シャープレシオの重み勾配を前もって求める必要がないのも、GA学習の強みです。
tradingrrl_.cppの25~29行目のベクター初期化記述と、121~134行目の入力ベクトルxとアクションFの算出記述を以下の様に書き換えてやります。
- 25~29行目のベクター初期化記述
x(T, vector<double>(M+2+9, 0.0)), F(T+1+9, 0.0), R(T, 0.0), w(M+2+9, 1.0), w_opt(M+2+9, 1.0),
- 121~134行目の入力ベクトル
xとアクションFの算出記述
void cppTradingRRL::set_x_F(){
for(int i=T-1 ; i>=0 ; --i ){
x[i][0] = 1.0;
x[i][M+2-1] = F[i+1];
for(int k=1 ; k<10 ; ++k ){
x[i][M+2-1+k] = F[i+1+k];
}
for(int j=1 ; j<M+2-1 ; ++j ){
x[i][j] = r[i+(j-1)];
}
double wdotx = 0.0;
for(int k=0 ; k<M+2+9 ; ++k ){
wdotx += w[k]*x[i][k];
}
F[i] = tanh(wdotx);
}
}
また、main.py内31~45行目のGA学習実施部分で、重みの変更範囲指定min_w、max_wの個数を9個増やしてやります。
#--- GA fit #--- Set w ranges. min_w = np.ones(M+2+9) * -3.0 max_w = np.ones(M+2+9) * 3.0 #min_w[0] = -5.0 #max_w[0] = 5.0 min_w[M+2-1:M+2-1+9] = -5.0 max_w[M+2-1:M+2-1+9] = 5.0 nind = 200 ngen = 20000 random_state = 64 best_ind, logbook = ga_fit(rrl, min_w, max_w, random_state, nind, ngen) rrl.w = best_ind rrl.calc_dSdw()
世代ループ数ngen = 20000で学習を行ってみます。
シャープレシオの推移
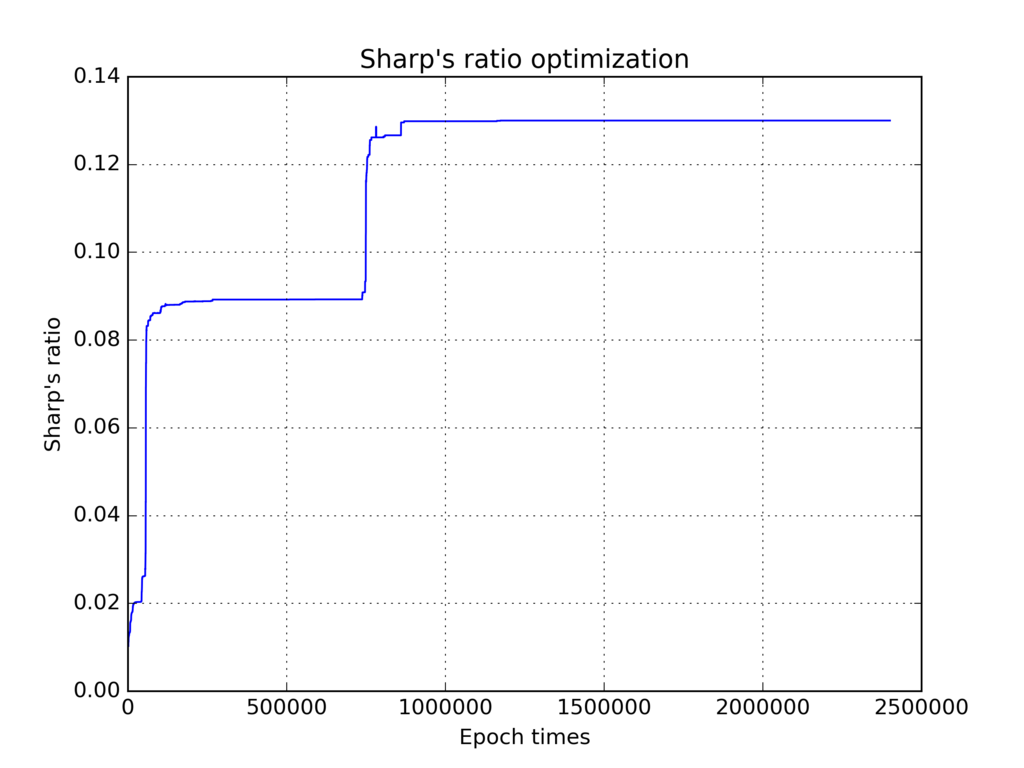
エポック数1000000回から、シャープレシオがアップデートされておらず、世代ループ数ngen = 20000は多すぎましたね。
過去の期間Tでの学習結果
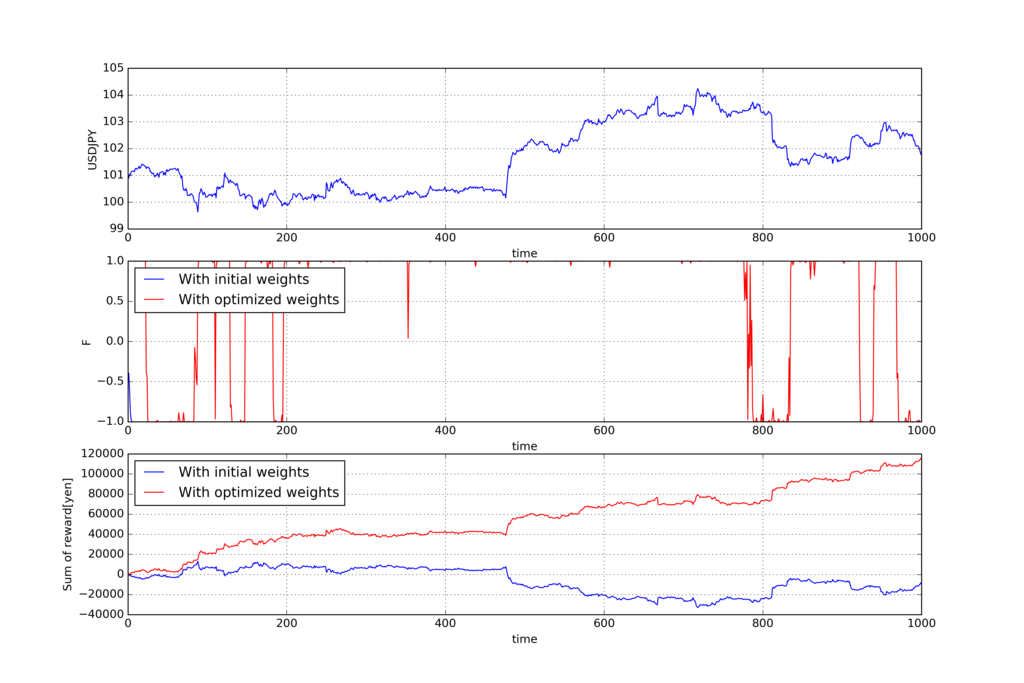
下段グラフの報酬の推移をみると、学習後はちゃんと右肩上がりになっているので、うまく学習できています。
未来の期間Tでの取引シミュレーション結果
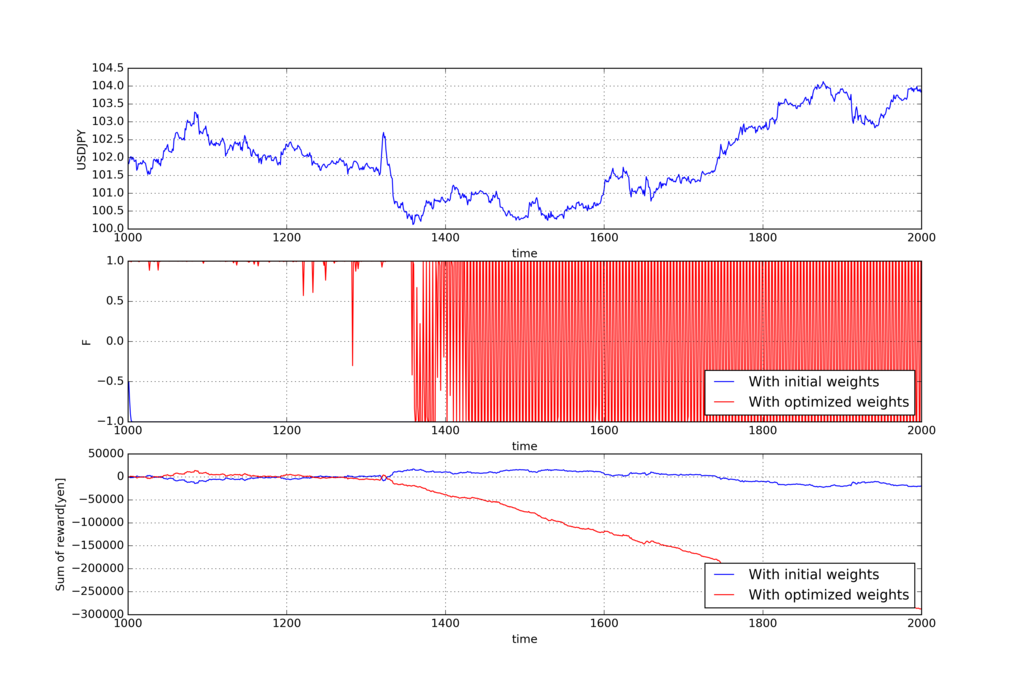
中段のグラフですが、エージェントのアクションが連続的に1になったり-1になったりしていてなんか怖いです。挙動不審になってますね。
下段グラフの報酬の推移も下がりまくっており、余計おバカになってしまいました。入力する過去データを増やしたからと言って、RRLエージェントが賢くなるわけではないんですね。。
まとめ
RRLの改造結果は散々でしたが、勾配上昇法と比べGAの学習効率はそこまで悪いわけではないですし、コスト関数の重み勾配を求める必要がないので、新しく開発した学習機の性能を手軽に調べることができるという点でGAでの学習は中々使えるのではないかと思います。
もう一点試してみたい事に、エージェントのアクションの決定を単純なパーセプトロンではなく、ディープなニューラルネットにしたらどうなるのかな?というのがあります。
今はまだ深層学習の知識が足りないですが、もっと勉強していつか試してみたいですね。